エンジンの開発・設計のために 熱力学の虎の巻!機械工学科
|
 |
|---|
2014.08.06
高校の物理でもボイル・シャルルの法則や熱の仕事当量など、温度や熱について学びます。熱と仕事の関係を論ずる物理学を熱力学といいます。大学の機械系学科では四力学(機械力学、材料力学、流体力学、熱力学)なるものがあり、そのどれもが必修科目となっています。流体力学や熱力学は、空気や熱という目に見えないものが学びの対象であるため、学生にとって親しみにくい科目であるようです。そんな熱力学はエンジンの開発・設計のために必要不可欠な学問でもあります。ここでは、大学でエンジンのことをもっと学び、将来は自動車に関わる仕事に就きたいと考えている皆さんに、エンジンの熱力学についてはこれさえ知っておけばなんとかなるさ、という秘伝の例題をお教えします。
図1に4ストロークガソリンエンジンのシリンダー内の容積と圧力の関係を示します。4ストロークエンジンのサイクルは吸気行程、圧縮行程、膨張行程、排気行程により構成されています。圧縮行程の終わりから膨張行程の始まりにかけてガソリンと空気の混合気を燃焼させます。
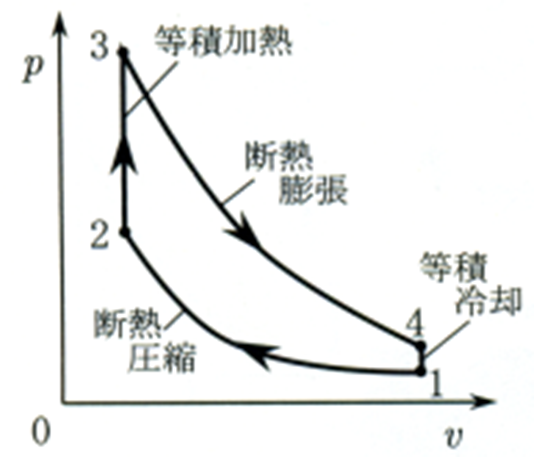
一方、熱力学でガソリンエンジンのサイクルを論ずるときには、オットーサイクルというものを用います。オットーとは、ガソリンエンジンのルーツを発明したドイツ人(Nicolaus August Otto)の名前です。オットーサイクルでは、図2に示すように、シリンダー内のガスの状態が状態1⇒状態2⇒状態3⇒状態4⇒状態1と変化します。そして、以下のように、各状態から次の状態への変化を実際のサイクルの行程に当てはめます。実際のサイクルではピストンの往復運動により燃焼ガスがシリンダー外に排出され、新たな混合気がシリンダー内に吸入されますが、オットーサイクルでは状態4⇒状態1の等積変化のもとで排気と吸気が行われると考えます。
・状態1⇒状態2の断熱変化: 実際のサイクルの圧縮行程
・状態2⇒状態3の等積変化: 燃焼による圧力上昇
・状態3⇒状態4の断熱変化: 実際のサイクルの膨張行程
・状態4⇒状態1の等積変化: 実際のサイクルの排気行程と吸気行程
以上のように考えると、状態1は吸気直後の混合気の状態、状態2は燃焼直前の混合気の状態、状態3は燃焼直後の燃焼ガスの状態、状態4は排気直前の燃焼ガスの状態となります。さて、各状態の混合気や燃焼ガスの圧力と温度はどの程度の値なのでしょうか?ここでは、計算を単純化するためにエンジンの圧縮比を8=2^3(ここでは2の3乗をこのように表します)、シリンダー内のガスの比熱比を1.333…=4/3と設定します。圧縮比8は最近のガソリンエンジンの圧縮比と比べると低い値ですが、あり得ない値ではありません。標準状態のもとで乾燥空気の比熱比は1.399、二酸化炭素の比熱比は1.286ですから、シリンダー内のガスの比熱比1.333…もおかしな値ではありません。これらの値を用いると、各状態の圧力と温度は以下のようになります。
・状態1の圧力p1=0.1 MPa、温度T1=300 K(大気の状態に設定)
・状態2の圧力p2=1.6 MPa、温度T2=600 K
・状態3の圧力p3=6.4 MPa、温度T3=2400 K(燃焼により温度が1800 K上昇するように設定)
・状態4の圧力p4=0.4 MPa、温度T4=1200 K
圧力は状態1の圧力⇒16倍⇒4倍⇒1/16⇒1/4と変化します.温度は状態1の温度⇒2倍⇒4倍⇒1/2⇒1/4と変化します。覚えやすい値ですね。これらの値を覚えておくだけでもシリンダー内のガスの状態を定量的に論ずることができるわけですが、さらにこれらの値を求める方法を覚えておけば、圧縮比や比熱比を変更すると各状態の圧力と温度はどのように変化するのか、それにより熱効率をどのように向上させることができるのか、論ずることができます。各状態の圧力と温度の計算方法を見ていきましょう。
状態1⇒状態2の断熱変化では、圧縮比V1/V2=2^3と比熱比γ=4/3を用いて圧力について16倍、温度について2倍という倍率を作ればいいわけです。断熱変化ではp1・V1^γ=p2・V2^γが成り立つため、p2=p1×(V1/V2)^γ=p1×(2^3)^(4/3)=p1×2^4=p1×16が求まります。また、T1・V1^(γ-1)=T2・V2^(γ-1)が成り立つため、T2=T1×(V1/V2)^(γ-1)=T1×(2^3)^(1/3)=T1×2が求まります。
状態2⇒状態3の等積変化では燃焼により温度が1800 K上昇すると、T3=T2+1800 K=2400 K=T2×4となります。等積変化ではp2/T2=p3/T3が成り立つため、p3=p2×(T3/T2)=p2×(2400 K/600 K)=p2×4が求まります。圧力も温度も4倍になります。
状態3⇒状態4の断熱変化では、圧縮比V1/V2=V4/V3=2^3と比熱比γ=4/3を用いて圧力について1/16、温度について1/2という倍率を作ります。断熱変化ではp3・V3^γ=p4・V4^γが成り立つため、p4=p3×(V3/V4)^γ=p3×(V4/V3)^(-γ)=p3×(2^3)^(-4/3)=p3×2^(-4)=p3×1/16が求まります。また、T3・V3^(γ-1)=T4・V4^(γ-1)が成り立つため、T4=T3×(V3/V4)^(γ-1)=T3×(V4/V3)^(1-γ)=T3×(2^3)^(-1/3)=T3×2^(-1)=T3×1/2が求まります。
状態4⇒状態1の等積変化ではp1=p4×1/4、T1=T4×1/4となり、圧力と温度は状態1の値に戻ります。
最後にオットーサイクルの理論熱効率について考えます。圧縮比を8、比熱比を1.333…と設定すると、オットーサイクルの理論熱効率は丁度50 %になります。これらの値を覚えておけば、オットーサイクルの理論熱効率がη=1-1/(V1/V2)^(γ-1)=1-1/(2^3)^(1/3)=1-1/2=0.5(百分率で表すと50 %)という式により求まることも覚えやすいのではないでしょうか。この式によれば、オットーサイクルの理論熱効率は圧縮比と比熱比のみで決まり、圧縮比または比熱比を大きな値に変更すると熱効率を向上させることができます。
いかがでしたか?ちょっと難しかったですか?しかし、以上の例題により得られる理解をさらなる知識や経験で味付けしていけば、皆さんもエンジンの専門家として活躍することができるでしょう。
図1に4ストロークガソリンエンジンのシリンダー内の容積と圧力の関係を示します。4ストロークエンジンのサイクルは吸気行程、圧縮行程、膨張行程、排気行程により構成されています。圧縮行程の終わりから膨張行程の始まりにかけてガソリンと空気の混合気を燃焼させます。
一方、熱力学でガソリンエンジンのサイクルを論ずるときには、オットーサイクルというものを用います。オットーとは、ガソリンエンジンのルーツを発明したドイツ人(Nicolaus August Otto)の名前です。オットーサイクルでは、図2に示すように、シリンダー内のガスの状態が状態1⇒状態2⇒状態3⇒状態4⇒状態1と変化します。そして、以下のように、各状態から次の状態への変化を実際のサイクルの行程に当てはめます。実際のサイクルではピストンの往復運動により燃焼ガスがシリンダー外に排出され、新たな混合気がシリンダー内に吸入されますが、オットーサイクルでは状態4⇒状態1の等積変化のもとで排気と吸気が行われると考えます。
・状態1⇒状態2の断熱変化: 実際のサイクルの圧縮行程
・状態2⇒状態3の等積変化: 燃焼による圧力上昇
・状態3⇒状態4の断熱変化: 実際のサイクルの膨張行程
・状態4⇒状態1の等積変化: 実際のサイクルの排気行程と吸気行程
以上のように考えると、状態1は吸気直後の混合気の状態、状態2は燃焼直前の混合気の状態、状態3は燃焼直後の燃焼ガスの状態、状態4は排気直前の燃焼ガスの状態となります。さて、各状態の混合気や燃焼ガスの圧力と温度はどの程度の値なのでしょうか?ここでは、計算を単純化するためにエンジンの圧縮比を8=2^3(ここでは2の3乗をこのように表します)、シリンダー内のガスの比熱比を1.333…=4/3と設定します。圧縮比8は最近のガソリンエンジンの圧縮比と比べると低い値ですが、あり得ない値ではありません。標準状態のもとで乾燥空気の比熱比は1.399、二酸化炭素の比熱比は1.286ですから、シリンダー内のガスの比熱比1.333…もおかしな値ではありません。これらの値を用いると、各状態の圧力と温度は以下のようになります。
・状態1の圧力p1=0.1 MPa、温度T1=300 K(大気の状態に設定)
・状態2の圧力p2=1.6 MPa、温度T2=600 K
・状態3の圧力p3=6.4 MPa、温度T3=2400 K(燃焼により温度が1800 K上昇するように設定)
・状態4の圧力p4=0.4 MPa、温度T4=1200 K
圧力は状態1の圧力⇒16倍⇒4倍⇒1/16⇒1/4と変化します.温度は状態1の温度⇒2倍⇒4倍⇒1/2⇒1/4と変化します。覚えやすい値ですね。これらの値を覚えておくだけでもシリンダー内のガスの状態を定量的に論ずることができるわけですが、さらにこれらの値を求める方法を覚えておけば、圧縮比や比熱比を変更すると各状態の圧力と温度はどのように変化するのか、それにより熱効率をどのように向上させることができるのか、論ずることができます。各状態の圧力と温度の計算方法を見ていきましょう。
状態1⇒状態2の断熱変化では、圧縮比V1/V2=2^3と比熱比γ=4/3を用いて圧力について16倍、温度について2倍という倍率を作ればいいわけです。断熱変化ではp1・V1^γ=p2・V2^γが成り立つため、p2=p1×(V1/V2)^γ=p1×(2^3)^(4/3)=p1×2^4=p1×16が求まります。また、T1・V1^(γ-1)=T2・V2^(γ-1)が成り立つため、T2=T1×(V1/V2)^(γ-1)=T1×(2^3)^(1/3)=T1×2が求まります。
状態2⇒状態3の等積変化では燃焼により温度が1800 K上昇すると、T3=T2+1800 K=2400 K=T2×4となります。等積変化ではp2/T2=p3/T3が成り立つため、p3=p2×(T3/T2)=p2×(2400 K/600 K)=p2×4が求まります。圧力も温度も4倍になります。
状態3⇒状態4の断熱変化では、圧縮比V1/V2=V4/V3=2^3と比熱比γ=4/3を用いて圧力について1/16、温度について1/2という倍率を作ります。断熱変化ではp3・V3^γ=p4・V4^γが成り立つため、p4=p3×(V3/V4)^γ=p3×(V4/V3)^(-γ)=p3×(2^3)^(-4/3)=p3×2^(-4)=p3×1/16が求まります。また、T3・V3^(γ-1)=T4・V4^(γ-1)が成り立つため、T4=T3×(V3/V4)^(γ-1)=T3×(V4/V3)^(1-γ)=T3×(2^3)^(-1/3)=T3×2^(-1)=T3×1/2が求まります。
状態4⇒状態1の等積変化ではp1=p4×1/4、T1=T4×1/4となり、圧力と温度は状態1の値に戻ります。
最後にオットーサイクルの理論熱効率について考えます。圧縮比を8、比熱比を1.333…と設定すると、オットーサイクルの理論熱効率は丁度50 %になります。これらの値を覚えておけば、オットーサイクルの理論熱効率がη=1-1/(V1/V2)^(γ-1)=1-1/(2^3)^(1/3)=1-1/2=0.5(百分率で表すと50 %)という式により求まることも覚えやすいのではないでしょうか。この式によれば、オットーサイクルの理論熱効率は圧縮比と比熱比のみで決まり、圧縮比または比熱比を大きな値に変更すると熱効率を向上させることができます。
いかがでしたか?ちょっと難しかったですか?しかし、以上の例題により得られる理解をさらなる知識や経験で味付けしていけば、皆さんもエンジンの専門家として活躍することができるでしょう。