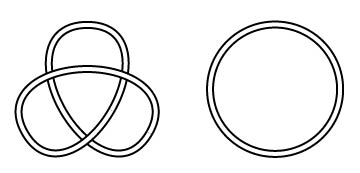応用数学特論一般教育科
|
 |
|---|
2015.11.28
皆さんは大学に入ると専門科目以外にも様々な科目を履修します。ここではちょっと先の話かもしれませんが、大学院生向けの科目を紹介したいと思います。我々一般教育科数学教室が担当しているのは「応用数学特論I・II」で、いずれも担当者がそれぞれの専門分野を生かした講義をしています。今回紹介する「応用数学特論I」ではここ数年「トポロジー」に関する講義をしています。物理や化学など、様々な分野で応用されているので、耳にしたことがあるかもしれません。
トポロジーは幾何学の一分野で、切ったり貼ったりしない限り図形を自由に変形してよいというルールで、様々な図形を分類するのが大きな目的です。講義においては1次元の(線でできた)図形や2次元の(平たい面でできた)図形を扱います。例えば図1の図形を見て下さい。トポロジーのルールに従えばこれらは同じ図形ですが、分かりますか?同じであることを証明するには、実際にどう変形するのかその手順を文章で説明したり、絵で描くことで示します。
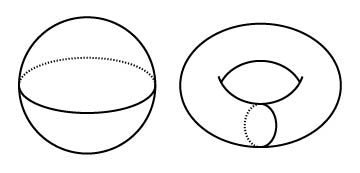
次に図2の図形を見て下さい。これらはトポロジーのルールに従えば異なる図形です。切ったり貼ったりできないということは穴を開けることもふさぐこともできないので、いくら変形しても左の図形を右の形にすることはできません。しかし、「いくらやってもできないから」というのは、異なる図形であると示したことにはなりません。「不変量」という、図形を変形しても変わらない(数学的な)値が必要になります。ここでは「オイラー標数」という不変量を使うと区別することができます。
講義ではこれまでの数学とは違って、図形の絵を沢山描いてもらいます。絵を描くのが苦手という方もご心配なく。美術の授業で描くような絵とは違いますし、どの学生も講義を受けていく中で十分上手になります。おそらくはこれまで受けたことのない講義ですし、頭の刺激にもなると思うので是非受講してみてください。
トポロジーは幾何学の一分野で、切ったり貼ったりしない限り図形を自由に変形してよいというルールで、様々な図形を分類するのが大きな目的です。講義においては1次元の(線でできた)図形や2次元の(平たい面でできた)図形を扱います。例えば図1の図形を見て下さい。トポロジーのルールに従えばこれらは同じ図形ですが、分かりますか?同じであることを証明するには、実際にどう変形するのかその手順を文章で説明したり、絵で描くことで示します。
次に図2の図形を見て下さい。これらはトポロジーのルールに従えば異なる図形です。切ったり貼ったりできないということは穴を開けることもふさぐこともできないので、いくら変形しても左の図形を右の形にすることはできません。しかし、「いくらやってもできないから」というのは、異なる図形であると示したことにはなりません。「不変量」という、図形を変形しても変わらない(数学的な)値が必要になります。ここでは「オイラー標数」という不変量を使うと区別することができます。
講義ではこれまでの数学とは違って、図形の絵を沢山描いてもらいます。絵を描くのが苦手という方もご心配なく。美術の授業で描くような絵とは違いますし、どの学生も講義を受けていく中で十分上手になります。おそらくはこれまで受けたことのない講義ですし、頭の刺激にもなると思うので是非受講してみてください。