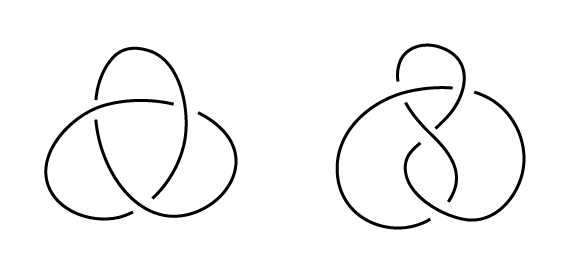結び目理論は位相幾何学（トポロジー）の一分野で、1950年頃から本格的に研究され始めた、比較的新しい数学です。研究の対象はとても単純なもので、図１のような絡まった輪っか（結び目）です。きっと初めて聞いた人は、「これの一体何が数学になるんだろう？」と思うことでしょう。この二つの結び目をどのように動かしても解くことができないことは、感覚的にはすぐに分かると思います。しかし、科学的に断定するためには理論的な根拠を明確に与える必要があります。この感覚に頼らない根拠として数学を用いているのですが、今回は難しい数学の話は飛ばして結び目理論の一端に触れてみましょう。

現在までに、結び目の性質を調べるための優れた方法がいくつも考案されています。今回は分かりやすさを主眼において、3彩色という方法を紹介します。これは名前の通りなのですが、図2のように結び目に3つの色（赤・青・黄）を塗ります。線同士が交差している箇所（交点）の周りがそれぞれ異なる3色で囲まれている、という状況になっている事を確認してください。「もしこのような塗り方が出来るのならば、その結び目は解けない」ということが数学的に証明されています。しかし、この3彩色は万能ではありません。例えば図１の右側の結び目は3色の塗り分けができないのですが、解けない結び目です。これが解けるか否かを明らかにするためには、また別の手法を用いる必要があるということです。

今回紹介したのは最も簡単な3彩色のみでしたが、結び目理論の様々な問題を解決するために、現在も活発に新しい手法が考案されています。このように、形としてはとても単純な輪っかが対象であるのに、現在の数学でも解決できないような問題がまだ無数に存在しています。「絡まり」という状況は、日常生活でもよく見られると思うのですが、そこにはとても複雑で面白い世界が広がっています。