組合せデザイン理論は、与えられた条件(均整やバランス)を満たす構造を設計・解析する離散数学の分野です。例えば、3人で対戦するゲームを7人で遊ぶ場合を考えましょう。公平に「1人3対戦ずつ」行い、さらに「自分以外の6人とは1回ずつ」対戦するような組合せを作るとします。7人をA,B,C,D,E,F,Gとすると
{A,B,D}, {B,C,E}, {C,D,F}, {D,E,G}, {E,F,A}, {F,G,B}, {G,A,C}
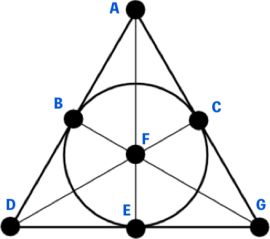
という7対戦分の組合せが作れます。この構造はFano平面と呼ばれる幾何構造と対応しています(図1)。7つの頂点には人が、7つの直線には対戦の組合せが対応します({B,C,E}は円状になっていますが一つの直線とみなします)。
このように、ある有限集合の要素を、決まったサイズの部分集合(これをブロックと呼びます)にまとめる構造をブロックデザインと呼びます。どの要素が何回出現するか、2つの要素のペアが何回一緒に現れるかといった条件はパラメータとして決められています。
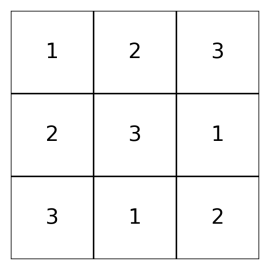
他にも、行・列・記号の出現を均等にするラテン方格も組合せデザインの代表例です。これは縦・横のどちらにも同じ記号が重複しないように配置した表です。図2の3×3 の場合は各行・各列には1,2,3が1度ずつ現れていることが確認できます。
ラテン方格は古くから知られていましたが、18世紀にオイラーが体系的に研究し、直交ラテン方格や「36人の士官問題」などの存在問題を通じて理論が発展しました。現在では、実験条件の割り当て、暗号・符号設計、情報通信など、幅広い分野で利用されています。
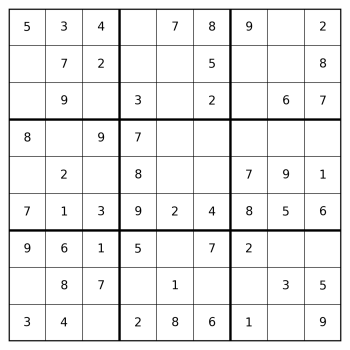
身近な例が 9×9 の数独です。数独はラテン方格を基礎構造とし、「縦・横で数字を重複させない」という性質に加えて、「3×3 の小ブロック内でも数字が重複しない」という条件を加えることで、より複雑で解き応えのあるパズルになっています(図3)。
組合せ構造は、スポーツ大会の日程を公平に組む、味覚試験で試料の順番を偏りなく割り当てる、通信データの誤りを検出・訂正するなど様々な場面で活用されています。応用分野は統計的実験計画法、暗号理論、符号理論、情報通信など多岐にわたります。
当研究室では、
- 新しいデザインの理論的構成法の研究
- コンピュータ探索や最適化アルゴリズムによる未知構造の発見
- 工学・情報科学など異分野への応用
などを行っています。 近年は組合せデザインを機械学習へ応用する研究も進めています。




